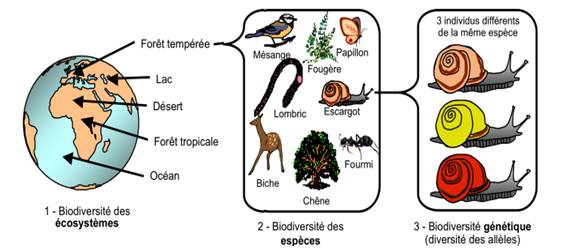
La biodiversité est la diversité des êtres vivants dans un milieu. Elle s’observe à l’échelle des écosystèmes (diversité écosystémique), des espèces (diversité interspécifique) et de la génétique (diversité intraspécifique). Une espèce est l’ensemble des êtres vivants qui partagent une combinaison unique de caractères morphologiques et moléculaires = ensemble des individus qui se ressemblent, se reproduisent entre eux et dont la descendance est fertile. Un gène est portion d’ADN qui contient une information génétique. Un allèle est une version d’un gène. On cherche à savoir comment la biodiversité évolue dans l’espace et le temps, en s’intéressant aux mesures de la biodiversité, à son évolution et au rôle des êtres humains sur cette évolution.
I. Mesure de la biodiversité
A. L’échantillonnage (activité 1)
La biodiversité se mesure par des techniques d’échantillonnage, par des prélèvements et des comptages d’individus de différentes espèces (=spécimens), ou même par prélèvement et analyse d’ADN présent dans l’environnement (ADNe = ADN environnemental). On peut ainsi estimer certaines composantes de la biodiversité d’un écosystème donné, comme :
- la richesse spécifique d’un milieu : c’est le nombre d’espèces présentes dans un écosystème.
- l’abondance (nombre d’individus) d’une population (= groupe d’êtres vivants de la même espèce présents dans un même endroit à un moment donné), d’une espèce, ou d’un plus grand groupe = taxon(= groupe d’individus présentant des caractères communs du fait de leur parenté ; ces groupes sont utilisés pour classer les êtres vivants) en comptant le nombre d’individus du groupe étudié.
On a estimé la richesse spécifique mondiale : il existe sur Terre un grand nombre d’espèces. Les scientifiques estiment cependant qu’une part importante de la biodiversité reste à découvrir car seule une faible proportion est connue.
L’effectif d’une population peut être estimée grâce à différentes méthodes à partir d’échantillons lorsque le comptage des individus n’est pas possible (trop abondants ou impossibles à observer tous en même temps), notamment la méthode CMR, et l’indice de confiance.

B. L’estimation de l’effectif par la méthode CMR (activité 2)
La méthode de capture-marquage-recapture (CMR) repose sur des calculs effectués sur un échantillon. On capture un nombre M d’individus qu’on marque. On relâche ces individus marqués dans la population d’origine. On recaptureensuite un nombre C d’individus, marqués ou non. Parmi ces individus recapturés, on compte R individus marqués. Si on suppose que la proportion d’individus marqués est identique dans l’échantillon de recapture et dans la population totale, donc que l’échantillon est représentatif de la population totale, l’effectif de la population totale s’obtient par un calcul de proportionnalité en calculant la quatrième proportionnelle (produit en croix):
Nombre total d’individus = nombre d’individus marqués x nombre d’individus recapturés/ nombre d’individus recapturés marqués
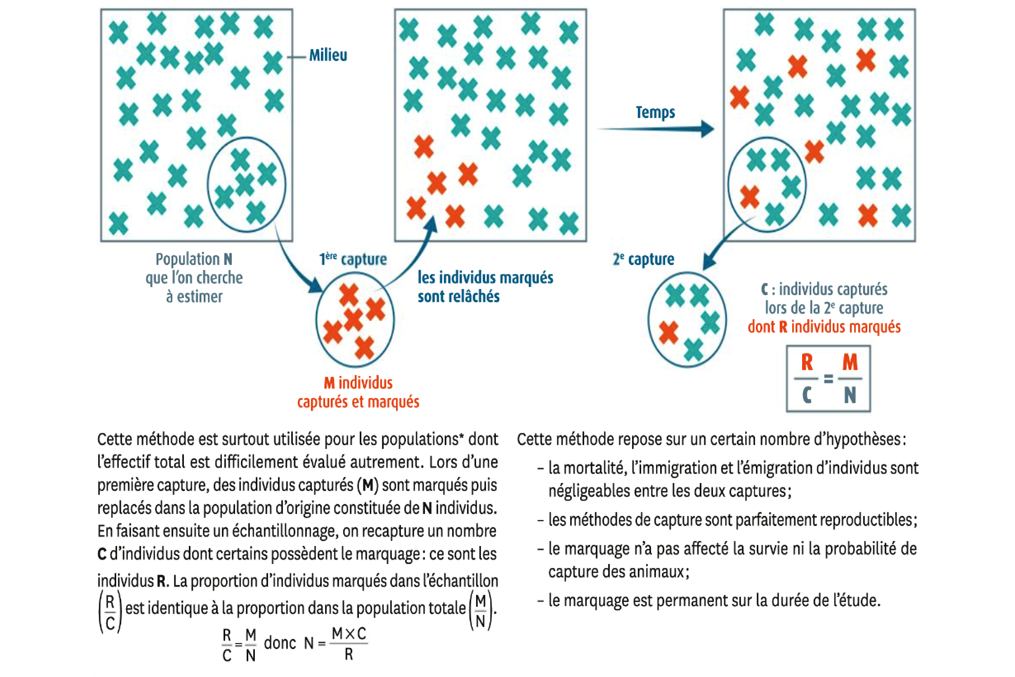
N = C x M / R
Avec :
- N l’effectif de la population (ce que l’on cherche)
- M le nombre d’individus marqués
- C le nombre d’individus recapturés
- R le nombre d’individus recapturés marqués
L’estimation est plus précise lorsque la taille l’échantillon augmente, en raison de la fluctuation d’échantillonnage. Ce type de calcul amène à un chiffre unique dont la précision ne peut être parfaitement fiable : on peut alors améliorer la fiabilité de l’estimation en réalisant la moyenne de plusieurs CMR, et/ou en encadrant cette valeur d’un intervalle de confiance qui contient la valeur obtenue par CMR.

Jeu sérieux pour s’entrainer: https://www.pedagogie.ac-nice.fr/svt/productions/capture
C. L’estimation de l’effectif par l’intervalle de confiance (IC)
À partir d’un seul échantillon, l’effectif d’une population peut également être estimé à l’aide d’un intervalle de confiance. L’intervalle de confiance inclut le nombre d’individus d’une population dans un intervalle compris entre un chiffre minimal et un chiffre maximal pour un niveau de confiance donné (c’est la probabilité que le nombre ou la fréquence réelle soit comprise dans cet intervalle). Pour calculer un effectif avec un intervalle de confiance, on calcule d’abord l’intervalle de confiance de la proportion d’un caractère, puis on en déduit l’intervalle de confiance de l’effectif.
- Calcul de l’intervalle de confiance d’une proportion : On mesure la fréquence f d’un caractère donné dans un échantillon n de la population avec :
f = nombre d’individus portant ce caractère / n
La valeur de f permet ensuite d’estimer la proportion p (la « fréquence réelle », non mesurable) de ce caractère dans la population totale avec une incertitude. On précise cette incertitude avec un intervalle de confiance (IC). Il y a 95% de chances que la proportion p d’un caractère soit contenue dans l’intervalle de confiance IC, pour n ≥ 30, n x f ≥ 5 et n x (1 – f) ≥ 5 :
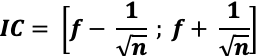
Pour une méthode CMR, f = R/C et n =C
- Calcul de l’intervalle de confiance d’un effectif (= nombre d’individus) : uniquement dans le cadre d’une capture-marquage-recapture, on peut en calculer l’intervalle de confiance à 95% dans lequel se trouve l’effectif de la population en reprenant le principe du calcul avec la méthode de CMR. On mesure f et n sur le 2e échantillonnage (la recapture) donc f = R/C et n = C. On sait que N = C x M / R. Or, la fréquence f des individus marqués dans l’échantillon vaut f = R / C , donc la formule ci-dessus donne : N = M / f. Comme f est assortie d’une incertitude, il y a 95% de chances pour que l’effectif de la population N soit compris dans l’intervalle de confiance IC :
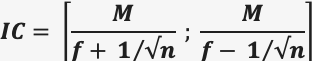
Dans le cas d’une méthode CMR, n = C et f = R/C.
NB : il existe d’autres formules donnant des résultats similaires.
Une estimation est toujours assortie d’un niveau de confiance (% de chances que l’effectif ou la proportion soit compris dans l’IC) strictement inférieur à 100 % en raison de la fluctuation des échantillons. Pour un niveau de confiance donné, l’estimation est d’autant plus précise que la taille de l’échantillon est grande.
II. Évolution de la biodiversité au sein des populations
L’évolution de la biodiversité génétique d’une population peut être mesurée par l’évolution de la fréquence des caractères. Elle est soumise aux forces évolutives : mutation, sélection naturelle, dérive génétique et migration. Pour déterminer dans quelle mesure un caractère donné dans une population est soumis à des forces évolutives, on recourt au modèle théorique de Hardy-Weinberg.
A. Stabilité des populations (activité 3)
Au cours de l’évolution, la composition génétique des populations d’une espèce change de génération en génération. Le modèle mathématique de Hardy-Weinberg utilise la théorie des probabilités pour décrire le phénomène aléatoire de transmission des allèles dans une population. En assimilant les probabilités à des fréquences pour des effectifs de grande taille d’après la loi des grands nombres, le modèle prédit que la structure génétique d’une population de grand effectif est stable d’une génération à l’autre sous certaines conditions (absence de migration, de mutation et de sélection naturelle ou de dérive génétique, reproduction aléatoire entre les individus) : la fréquence d’un caractère est stable et peut être calculé mathématiquement d’une génération à l’autre. Cette stabilité théorique est connue sous le nom d’équilibre de Hardy-Weinberg.
Démonstration : Le génotype correspond aux 2 allèles portés par un individu, l’un provenant du gamète de l’organisme paternel, l’autre du gamète de l’organisme maternel. Dans une population, pour un gène à 2 allèles A et a, les individus sont de génotype (AA), (Aa) ou (aa). On note dans la génération n d’une population :
- N le nombre d’individus de la population
- n(AA) le nombre d’individus de génotype (AA) et f(AA) la fréquence des individus portant les allèles (AA) dans la population ; f(AA) = nombre d’individus de génotype (AA) dans la population / nombre d’individus total de la population = n(AA)/N
- n(Aa) et f(Aa) le nombre et la fréquence des individus portant les allèles (Aa) dans la population ; f(Aa) = n(Aa)/N.
- n(aa) et f(aa) la fréquence des individus portant les allèles (aa) dans la population ; f(aa) = n(aa)/N.
- p la fréquence de l’allèle A dans la population : p = nombre d’allèles A dans la population / nombre d’allèles totaux dans la population. Sachant que les individus (AA) possèdent 2 allèles A, et les individus (Aa) possèdent un seul allèle, et qu’il y a 2 fois plus d’allèles que d’individus dans la population : p = [2 n (AA) + n (Aa)]/ 2N
- q la fréquence de l’allèle a dans la population ; q = [2 n (aa) + n (Aa)]/ 2N
Par définition, comme il n’y a que 2 allèles, p + q = 1
On peut alors calculer la fréquence de chaque allèle à partir de la fréquence des génotypes (=ensemble des allèles) des individus si on connaît le nombre d’individus de chaque génotype :
- la fréquence de l’allèle A est de p = 2 n(AA)/2N + n(Aa)/2N = f(AA) + f(Aa)/2
- la fréquence de l’allèle a est de q = 2 n(aa)/2N + n(Aa)/2N = f(aa) + f(Aa)/2
- q + p = 1 car il n’existe que ces 2 allèles donc 100% des possibilités ont été envisagées.
| Gamète mâle/Gamète femelle | (A) p) | (a) q |
| (A) p | (AA) p2 | (Aa) pq |
| (a) q) | (Aa) pq) | (aa) q2 |
La fréquence f des génotypes dans la population à la génération suivante n+1 est de :
f (AA)(n+1) = p2
f (Aa) (n+1) = 2pq
f (aa) (n+1) = q2
Dans cette génération n+1, les allèles A et a sont à la fréquence :
p(n+1) = f(AA) + f(Aa)/2 = p2 + 2pq/2 = p2 + pq. Or, q = 1 – p, donc, en replaçant q, l’équation devient :
p(n+1) = p2 + p(1-p) = p2 + p – p2 = p
On montrerait de même que q(n+1) = q
Donc, si les conditions de Hardy-Weinberg sont respectées (donc pour une population de grande taille et pour un gène qui n’est soumis à aucune force évolutive), la fréquence des allèles est stable au cours des générations, et les fréquences calculées correspondent aux fréquences théoriques.
B. Évolution des populations
Dans une population naturelle, les écarts entre les fréquences observées sur une population naturelle et les résultats du modèle s’expliquent notamment par les effets des forces évolutives :
- la mutation : elle fait apparaître un nouvel allèle qui n’existait pas avant si elle se produit dans les cellules germinales et est transmise aux générations suivantes.
- La sélection naturelle : elle diminue la fréquence d’un allèle moins avantageux = favorable pour la survie et/ou la reproduction de l’individu car les individus porteurs de l’allèle désavantageux ont une survie et/ou une reproduction réduite, et donc leur fréquence diminue (et réciproquement).
- la dérive génétique : elle fait varier au hasard la fréquence d’un allèle ayant peu d’impact sur la survie et/ou la reproduction de l’individu et qui n’est donc pas ou peu soumise à la sélection naturelle. Son effet est plus fort dans les populations de petite taille.
- la migration : certains individus se déplacent vers une autre région de façon permanente. Si ce groupe comporte une fréquence d’allèles différente de la population initiale, la fréquence des allèles dans la population restante est modifiée. (La recherche de nourriture n’est pas une migration, c’est l’étendue du territoire).
Toutes ces forces font varier les proportions des différents allèles et peuvent déplacer l’équilibre de Hardy-Weinberg voire amener un allèle à disparaître. Un écart de fréquence des allèles par rapport aux proportions théoriques calculées avec le modèle de Hardy-Weinberg traduit donc qu’une force évolutive s’exerce sur la population.
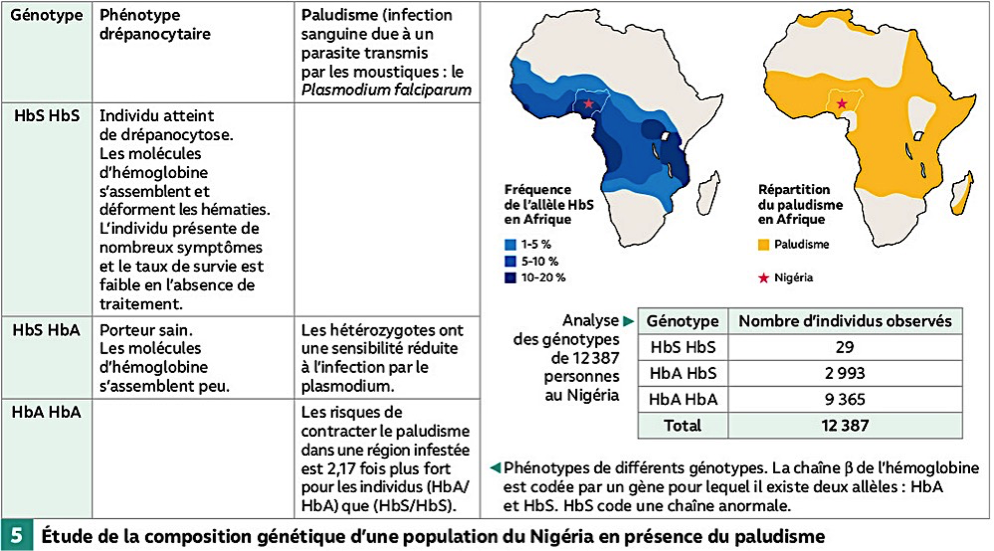
Ex: dans l’anémie falciforme humaine, la fréquence anormalement élevée de l’allèle responsable de la maladie dans les régions où le paludisme a une forte prévalence s’explique par l’avantage que confère aux hétérozygotes (HbS/HbA) l’allèle HbS responsable de l’anémie falciforme dans la survie à la maladie du paludisme: ici la sélection naturelle déplace l’équilibre en favorisant la survie des hétérozygotes.
III. L’impact des activités humaines sur la biodiversité
A. La diminution de la biodiversité
Les activités humaines (pollution, destruction des écosystèmes, combustions et leurs impacts climatiques, surexploitation d’espèces…) ont des conséquences sur la biodiversité, (notamment l’abondance et la richesse), et conduisent à l’extinction d’espèces.
La fragmentation d’une population en plusieurs échantillons de plus faibles effectifs entraîne par dérive génétique un appauvrissement de la diversité génétique d’une population. Celle-ci devient alors plus sensible aux maladies et est moins apte à s’adapter à un changement de son écosystème.
Exemple: le lynx ibérique est en déclin en raison de la fragmentation de son habitat et du piégeage http://www.iberlince.eu/index.php/eng/

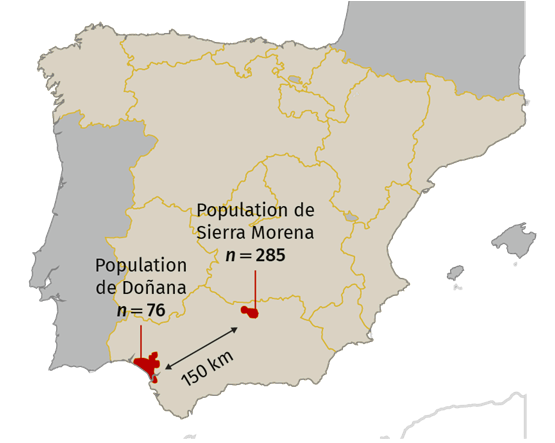
Un lynx ibérique ; localisation des populations de lynx ibérique
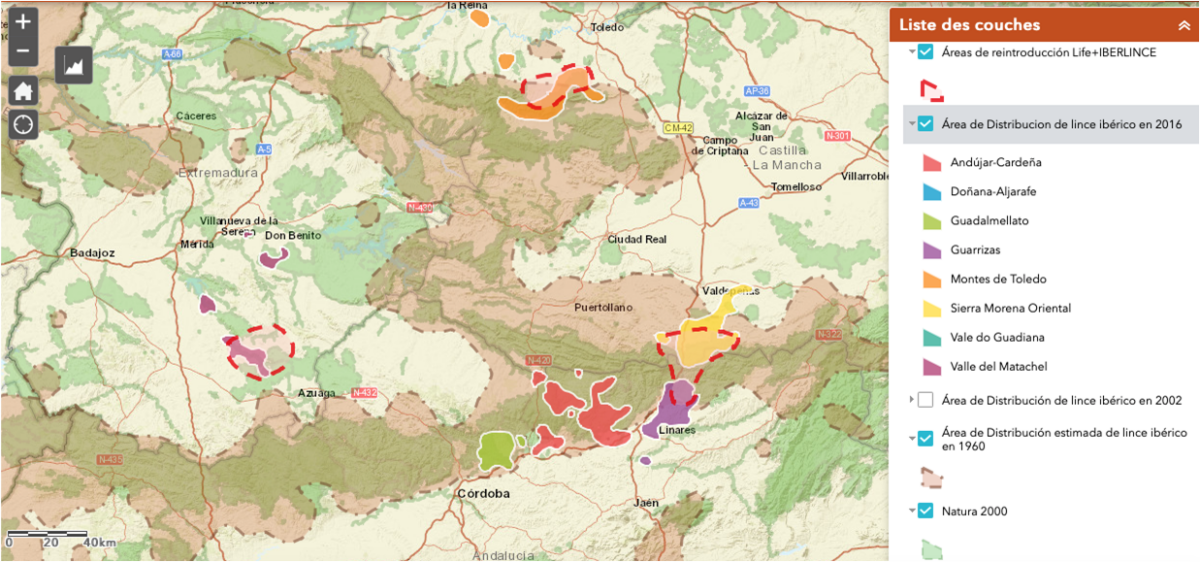
Fragmentation de l’habitat des lynx ibériques en 2016 et mise en place du réseau Natura 2000
B. La préservation de la biodiversité
La connaissance et la gestion d’un écosystème permettent d’y préserver la biodiversité. On peut ainsi restaurer en partie la continuité entre des écosystèmes avec des corridors écologiques permettant le déplacement des animaux entre des espaces fragmentés, les échanges d’individus entre populations pour accroitre les échanges génétiques, la protection des espaces naturels qui restaurent le fonctionnement des écosystèmes.
Ex: le réseau Natura 2000 protégeant les écosystèmes, l’amélioration de la sécurité des routes, les échanges génétiques ont permis de restaurer en partie la diversité génétique et d’augmenter l’abondance du lynx ibérique.
Conclusion
La biodiversité est mesurée grâce à des techniques d’échantillonnages qui permettent d’estimer une abondance et une richesse biologique grâce à des outils mathématiques. Les écarts à l’équilibre de Hardy-Weinberg montrent l’existence de forces évolutives. L’être humain, par ses activités, peut faire varier l’effet de ces forces évolutives et perturber ou protéger la biodiversité.
Pour les passionnés (et mélomanes): une interview du président du Museum d’Histoire Naturelle https://www.francemusique.fr/emissions/musique-emoi/bruno-david-naturaliste-president-du-museum-d-histoire-naturelle-91974
